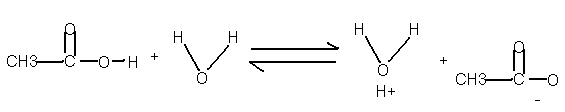
What are KA and pKA
To understand KA and pKA you first have to understand electrolytes.
Strong electrolytes- electrolytes that dissociate completely in aqueous solutions (e.g. NaCl, KCl, CaCl2).
NaCl(aq) ® Na+ (aq)+ Cl- (aq)
HCl(aq) + H2O ® H3O+ (aq)+ Cl- (aq)
No mater how much salt (or hydrochloric acid) you put in the solution it will dissociate into ions until of course it reaches saturation
Weak electrolytes – electrolytes that don’t completely dissociate but reach an equilibrium between the ionized and unionized form.(e.g. most organic acids)
CH3COOH(aq) + H2O «
CH3COO- (aq) + H3O+ (aq)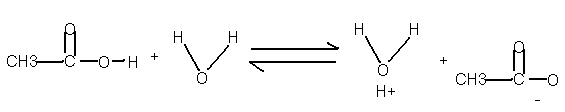
These species exist in solution at an equilibrium. If you add more acid the equilibrium shifts to the right. If you add more acetate ion (CH3COO- ) the equilibrium shifts to the left. ( La Chatlier’s Principle) But the ratio of products on the right to the acid on the left is constant; to be exact it is called an equilibrium constant Ka. Defined as follows
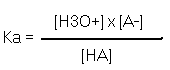
The weaker the acid the less products there will be on the right of the equilibrium so the numerator of this ratio will be small and the denominator large. Hence Ka will be small.
(small number divided by large number = small number).
These numbers get so small that chemists decided to make a scale similar to the pH scale because it is easier to deal with numbers like 4 or 3.4 instead of numbers like .0001 or 2.3x 10^3.2 ect. This scale is the pK scale. All that this entails is taking the negative log of the Ka.
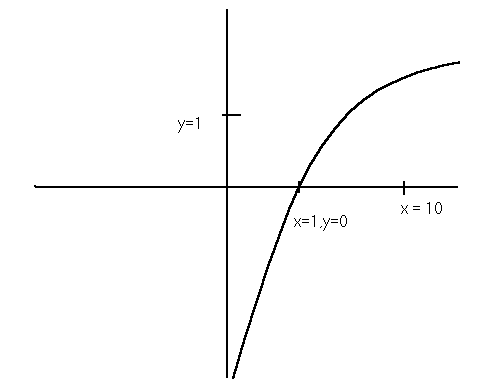
This is a graph of y = log x . The important landmarks are pointed out. What this graph tells us is that if you plug in a number for x, you will get a corresponding number for y on this curve. We are mostly concerned with the area between x=0 and x=1 as x approaches zero y becomes negative and x gets very close to zero but never touches because log 0 is undefined. So as x gets smaller and smaller y approaches negative infinity. So if you take the negative log of a very small number you get a very big number. Try this on your calculator take the log of .0000000002. Then take the negative of that number. You get 9.6………. so this means that if the Ka is very small (weak acid, then the pKa will be large. So the larger the pKa’s the weaker the acid.
Another interesting thing about pKa’s is that as we said in class if the pH of a solution is equal to the pKa then there is an equal amount of ionized to unionized species in other words at equilibrium [HA] = [A-]. And this can be illustrated by a simple equality.
If pKa = pH then –log [H3O] [A] / [HA] = - log [H3O]
Then that means [H3O] [A] / [HA] = [H3O] so [A]/[HA] =1 and they must be equal to each other for there ratio to be 1.
Now if you can’t remember if pKa higher than pH gives you more unionized or less unionized just set it up as an inequality.
pKa >pH
–log [H3O] [A] / [HA] > - log [H3O]
divide both sides by –1 to get rid of the negative sign. This will reverse the inequality. (we can see this is a truism in math by using a simple example: if –3 > - 4 then divide both sides by –1 we get 3 < 4)
log [H3O] [A] / [HA] < log [H3O]
[H3O] [A] / [HA] < [H3O] divide both sides by [H3O]
[A] /[HA] < 1 multiply both sides by [HA]
[A-] < [HA] so there is more unionized than ionized
This is the same thing that we said in class. I know that I didn’t put in the plus and minus signs for the A and H3O but my hands are getting tired. I apologize for the mistake on the previous tutorial. By trying to save keystrokes I skipped a step and made an error.
FMc 8/19/99